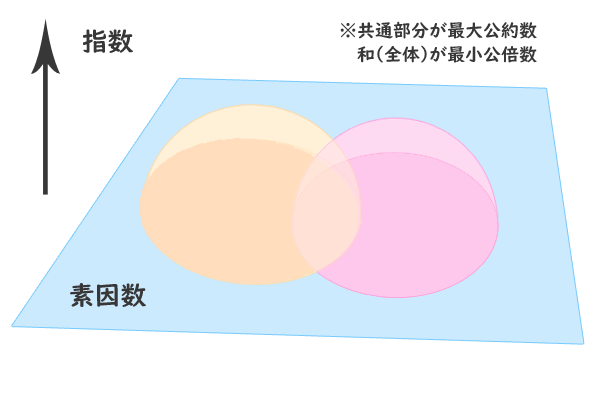
高校数学 最大公約数 最小公倍数です。 53番の問題です 答えは(a、b)=(6、270)、(30、54)です 求め方はわかるのですが、途中の(a´、b´)の時点で、(3、15)と考えてしまい答えが3つになってしまいます(a´b´は45) どうして(3、15)と考えてはいけないのでしょうか 回答お願いします 最大公約数・最小公倍数の公式 (l=ga'b'やab=gl)のイメージを確認しよう 高校数学Aの整数分野で、最大公約数・最小公倍数について取り扱います。 本格的に学習するのは小学校以来ということもあり、きちんとイメージを把握した上で学習することが重要な補足:最小公倍数も求めてみよう (1問目) 取り出し方の組合せ このような問題でよく最大公約数や最小公倍数を使うのですが、どういう時に使い分けるのですか? ここら辺の問題が苦手でどういう時に最大公約数を使い、どういう時に最小公倍数を使う
3
最大公約数 最小公倍数 問題 高校
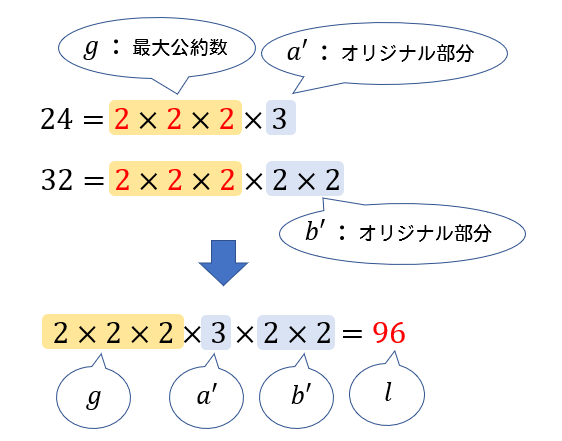
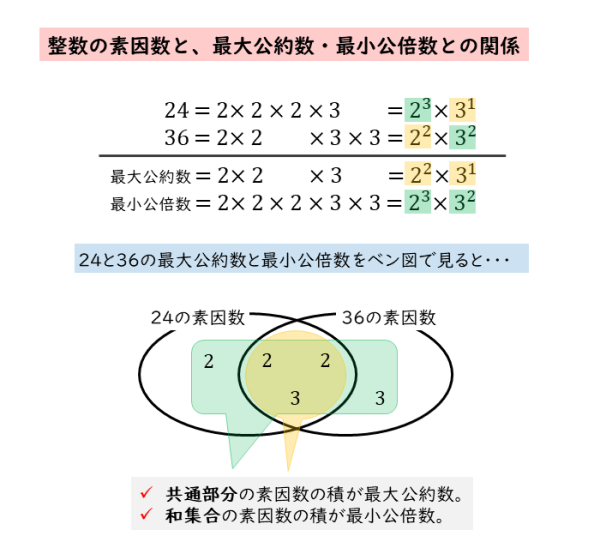
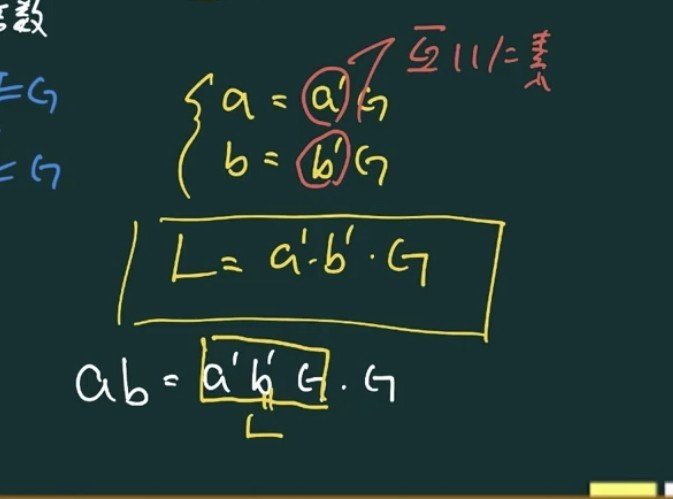
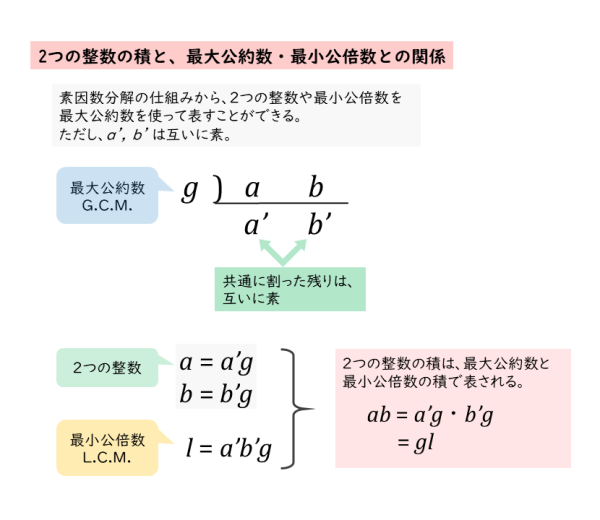
最大公約数 最小公倍数 問題 高校- 問題は、 「最大公約数と最小公倍数の和が51となるような2つの自然数の組をすべて求めなさい」 というものです。 これは、2つの自然数とその最大公約数、最小公倍数との関係を知らないと取り付き難い問題です。 すると、 A=aG B=bG と表せます。 2つの正の整数 a, \ b の最大公約数を g, 最小公倍数を l とする。 a=a'g, b=b'g ( a' と b' は互いに素な自然数) l=a'b'g gl=ab ただ、これらの性質って式で見てるだけではイメージがつかみにくいよね (^^;) なので、冒頭で具体例としてあげた 24 と 36 の




高校数学 数a 勉強動画 最大公約数 最小公倍数 の問題 19ch
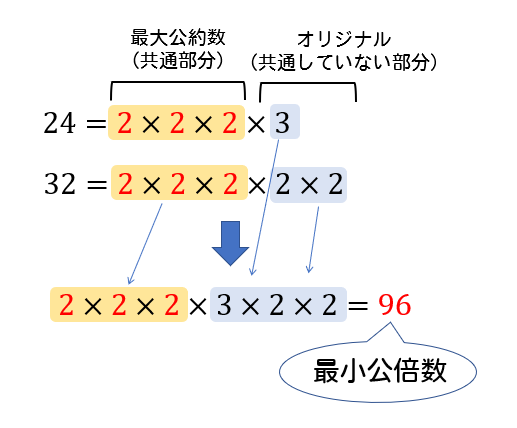
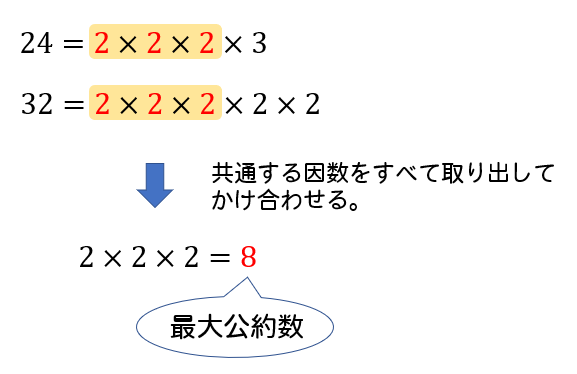
前回 https//googl/yfbWer 次回 https//googl/2ROjaU動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が質問一覧 75と135の最大公約数と最小公倍数がわかりません。どなたか教えてください。 それぞれ素因数分解 75=3×5² 135=3³×5 共通部分が最大公約数になる、 3が一つ、5が一つが両方に共通してるので 最大公約数は3×5=15 最小公倍数は、共通部分に、それぞれの共通してない部分を賭け合 あなたは最小公倍数とは何かわかりますか? 答えに困ってしまった人、この記事で確認していきましょう。 答えられた人も、もしかしたら最小公倍数の性質を全てはわかっていないかもしれません。 この記事では、最小公倍数の意味や求め方といった基礎の解説から始まり、から、大学
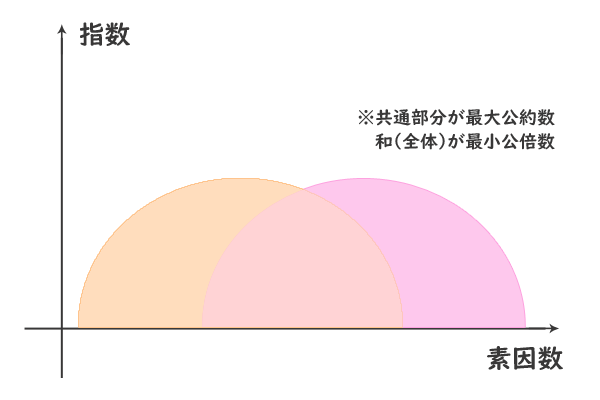
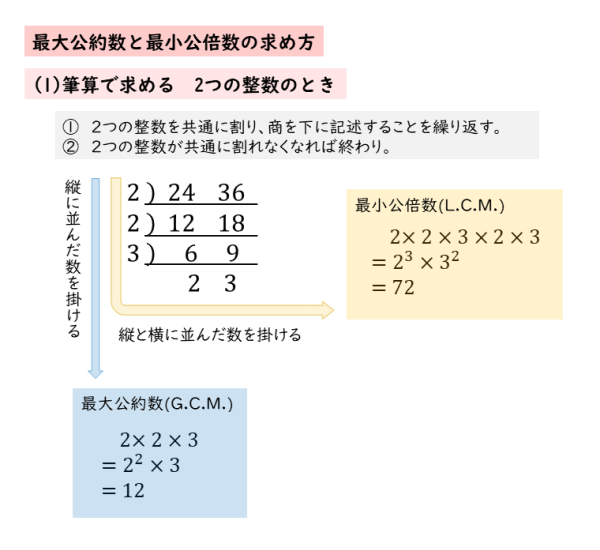
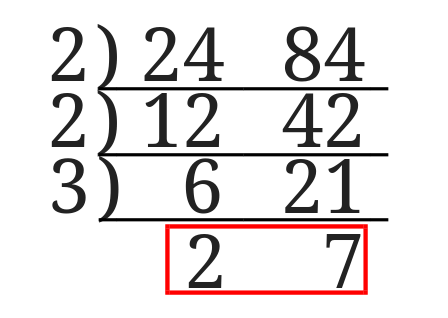
最小公倍数 を求める方法は,これと同様ですが,割った数と残った数を掛けます. 例 次の例で, 12, 18 の最大公約数は 6 , 18, 27 の最大公約数は 9 です. また, 12, 18 の最小公倍数は 36 , 18, 27 の最小公倍数は 54 です. 最大公約数と最小公倍数の関係 さて、ここまで公約数と公倍数についてみてきましたが、実はこの2つには大きな関係があります。 それは A = G a , B = G b で( a, b は互いに素、 G は最大公約数) A, B の最小公倍数が L であるとき L = G a b である。 最大公約数は自動的に正の数になる \\ 2zh なお,\ 1つでも0を含むときは公倍数が0になるので,\ この場合の最小公倍数を0と定める \\ 1zh 定理 1,\ 2は高校数学では自明としてよいが,\ よく知られた証明を示しておく \\ 2zh 上級者以外はスルーしてよい
中学受験の算数・理科ヘクトパスカルによる「最大公約数と最小公倍数の問題」の手書き解説です。 ある整数Aと72の最大公約数は12です。これについて,次の問いにこたえなさい。 (1) この2つの整数の最小公倍数が360であるとき,Aはいくつですか。 以上により、最大公約数が 、最小公倍数が である 数は となります。 最大公約数と最小公倍数の説明のおわりに いかがでしたか? ここで紹介した応用問題にあるように、最大公約数や最小公倍数を方程式として扱えるようになることが大切です。これを利用して、最大公約数を求める方法のことを ユークリッドの互除法 、または 互除法 といいます。 例えば、629と259の最大公約数を求める場合。 >最大公約数、最小公倍数の求め方と性質をイチ




24と180の最小公倍数 最大公約数を求める問題で 写真に書いてあるやり方でも解けま Clear



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
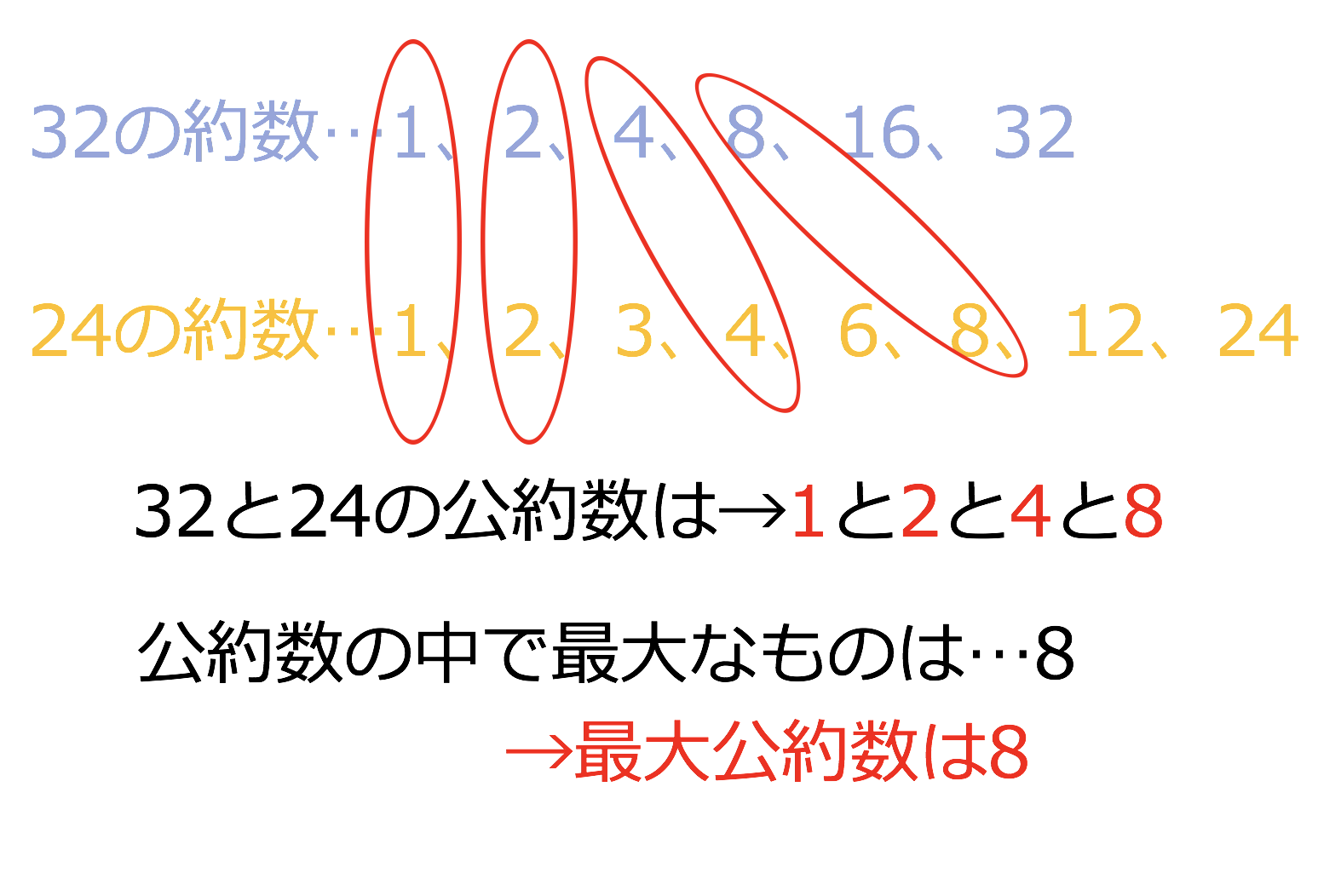
例 12 と 18 の公約数は, 1,2,3,6 で, 6 が最大公約数 2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを最小公倍数といいます. (1問目) 取り出し方の組合せ G次の等式を満たす自然数x, yの組をすべて求めよ。 このような このような問題でよく 「数の入門と算数 」シリーズは今回で 完結 です。 最終回 のテーマは「 素因数分解 , 約数の個数と総和 , 公約数と公倍数 」です。 前々回( 約数と倍数 素数と素因数分解 ) 、 前回( 指数のしくみ 約分と素因数分解 ) 、と続いてきた「 素因数分解 3 部作 」の 完結編 になります。 そんな最小公倍数を今回は徹底的に解説していきます。 最小公倍数の求め方は、小学生・中学生・高校生レベルそれぞれ用意しています。 ぜひ最後まで読んで、自分にあった求め方を見つけてみてください! 同じタイミングで習う 最大公約数 の説明は




ここのa とb が何を表してるのか教えてください Clear




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場
高校範囲・大学受験レベルの最大公約数、最小公倍数の問題は以下のように扱ってください。 結論としては、各数字を素因数分解をしたときの、 ・最大公約数:それぞれで、指数の 一番小さいものを拾い上げたもの ・最小公倍数:それぞれで、指数の最小公倍数を求めるためには,「すべての素因数」 2, 3, 5, 7 に「最大の指数」 2, 3, 2, 1 を付けます. L=2 2 ×3 3 ×5 2 ×7 → 3 III ユークリッドの互除法による方法 上に示した2つの方法は,「共通な約数が分かる場合」「素因数分解できる場合」に使えますその時に通分の場面で最小公倍数が使われない ということが起こる。さらに,部分分数の分解 ということも学ぶがそれにも支障を来すことに なる。 まとめ 今や小学校5年から学び始める最大公約数・ 最小公倍数の概念は中学校でも高校でも度々使




最大公約数と最小公倍数を求める 2 3 素因数分解を利用する 自由研究ノート 仮




中学数学より4 教科書に登場しない最小公倍数 最大公約数 身勝手な主張
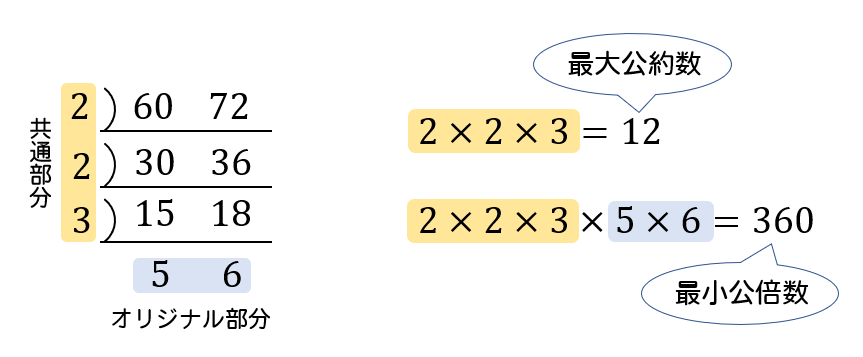
最大公約数と最小公倍数の求め方のコツ 例72と132の最大公約数と最小公倍数を求めよ。 解法基本素因数分解で処理していくのですが, 最大公約数は以下の画像にも書いてますが, 共通する素数の指数部の小さい方を選択します。ポイントの解説授業 これまで最小公倍数、最大公約数の求め方のコツを学習してきたね。 これらの知識を活用すると、次のような問題も解けるようになるよ。 例 nを正の整数とするとき、nと6の最小公倍数が12となるようなnをすべて求めよ。 単純に最小(3)255、459、1122の最大公約数は です。 (4)36、60、84の最小公倍数は です。 (5)2けたの整数で、6の倍数で144の約数でもあるのは 個あります。



最大公約数と最小公倍数の計算方法 高校数学マスター



最大公約数と最小公倍数
高校数学 最大公約数 最小公倍数です。 53番の問題です 答えは(a、b)=(6、270)、(30、54)です 求め方はわかるのですが、途中の(a´、b´)の時点で、(3、15)と考えてしまい答えが3つになってしまいます(a´b´は45) どうして(3、15)と考えてはいけ 最小公倍数は最大公約数に互いに素である部分を全てかけたものです 公式で書くと L(最小公倍数)=a1×b1×G a×b =a1×b1×G×G a1×b1×G=Lなので a×b =L×G=最小公倍数×最大公約数 しかし、これでは解けない問題がでてきます。 この問題どうしますか? 数字2講 最大公約数・最小公倍数(1節 約数と倍数) 問題集3章 整数の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん
最大公約数と最小公倍数を求める問題です。 179は分かりましたが180がわかりません。 何がわからないかもはっきりわかりません、助けてください。 1791 (D , 44 (2) 75 105 (3) 264, 924 42円 244 15,525, 1/ 32, 1848 ,924 /32, 462 66,231 5135 2110,22 525 2 ×5×1/ 5 7 3連絡先 kantaro@momosonetnejpツイッター http//twittercom/Kantaroお勧め動画自然対数の底e ネイピア数を東大留年美女&早稲田2つの数の最大公約数と最小公倍数を作るプログラムをつくります。 最大公約数 まず、ある数の約数をすべてリストアップすることを考えます。CindyScriptのリスト処理をする関数を使うと次のように簡単にできます。 yaku=select(1n,mod(n,#)==0);




最大公倍数 最小公約数の問題です 両方の解説をお願いします 1 18 54 Clear



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス
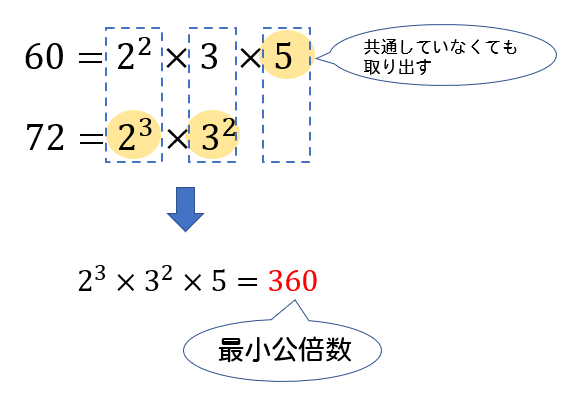
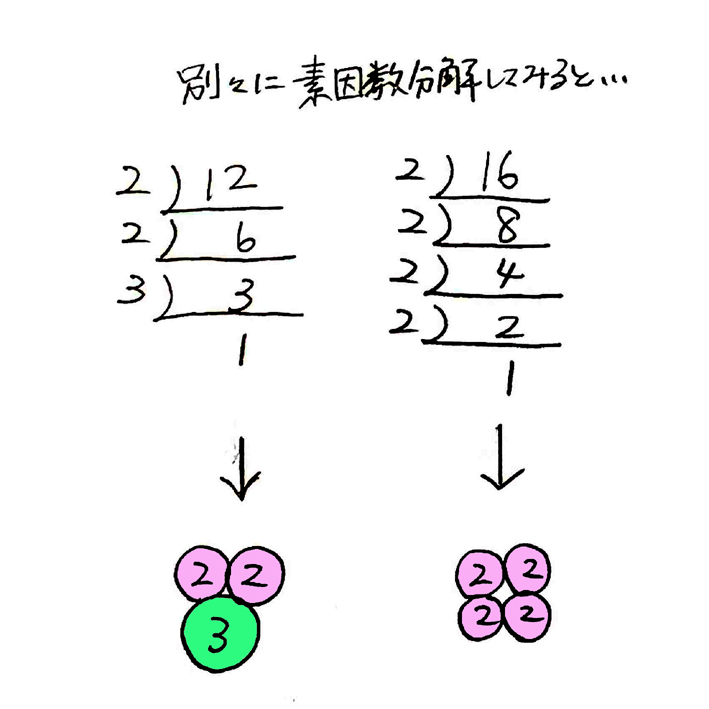
補足:最小公倍数も求めてみよう 最大公約数は素因数分解で得られた指数の小さい方を選んでそれらを掛け合わせました。 最小公倍数はその逆です。 つまり、指数の大きい方を選んでそれらを掛け合わせます。 では、先ほどと同様に108と56の最小公倍数高校受験において、整数の性質を知っておかないと解くことが困難な問題は多くあります。例えば以下の問題。皆さんは解けますか? (1) 5で割ると1あまり、6で割ると2あまる自然数のうち、0に最も近いものを求めよ。 (2) 2つの自然数の最小公倍数は100で最大公約数は5である。



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質




高校数学a 最小公倍数の求め方 練習編 映像授業のtry It トライイット




整数の性質が超わかる 最小公倍数 最大公約数の求め方 高校数学 A Youtube




鈴木貫太郎 בטוויטר 開成高校出身のイケメン秀才京大院生の古賀さんに開成高校の入試問題解説で褒められた 嬉しい 開成高校 整数問題 最大公約数 最小公倍数 T Co Ig68hzms5y 古賀さんのチャンネルhttps T Co Do1rjhdhcj T Co Atxisw1i0e




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




高校数学 数a 69 最大公約数 最小公倍数 Youtube



数学i Aチェック リピート 第6章 3整数の性質 2 最大公約数 最小公倍数 Pukiwiki




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場



48s96ub7b0z5f Net Yukuriddo Gojoho Kihon




最高の公倍数 公約 数 子供のための最高のぬりえ




数学a 最大公約数と最小公倍数の関係式の使い方とコツ 教科書より詳しい高校数学



高校数学aの問題です 和が168 最小公倍数が1001を満 Yahoo 知恵袋



最大公約数と最小公倍数



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数 最小公倍数の求め方 小学生算数指導にも役立ちます 塾講師ステーション情報局




最大公約数と最小公倍数 オモワカ整数 4 全21回 数学専門塾met Note




高校数学a 最小公倍数をヒントにnを求める問題 例題編 映像授業のtry It トライイット



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算




高校数学a 最大公約数と最小公倍数の定義 受験の月




練習15 16を教えて下さい お願いします Clear



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



中学受験の問題です 最小公倍数 最大公約数に関する添付の問題なの Yahoo 知恵袋



3



3つの自然数abc A B C について Aとbとcの最大公約数は12 Yahoo 知恵袋




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学



高校数学 Aの最大公約数 最小公倍数の問題です 全くわからないのでどなた Yahoo 知恵袋




高校数学 数a 勉強動画 最大公約数 最小公倍数 の問題 19ch




最高 6 と 9 の 公約 数 壁紙 配布



高校数学 解説動画 数学a 整数の性質 最大公約数 文章題 数学




高校数学a 最小公倍数をヒントにnを求める問題 練習編 映像授業のtry It トライイット




最大公約数 最小公倍数の公式 L Ga B やab Gl のイメージを確認しよう あんず学習塾のメモ 図表置き場



3




3つの整数の最大公約数と最小公倍数を求める問題 Clear



これの最大公約数と最小公倍数の求め方を教えてください 104 2 x131 Yahoo 知恵袋




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学



最大公約数と最小公倍数 オモワカ整数 4 全21回 数学専門塾met Note




高校数学a 最小公倍数の求め方 映像授業のtry It トライイット



1



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



高校数学の数aの問題です 最大公約数と最小公倍数のところです この問題 Yahoo 知恵袋




開成高校 整数問題 最大公約数 最小公倍数 Youtube




高校1年生の数学i 最大公約数 最小公倍数 について なぜこのような 数学 教えて Goo




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



48s96ub7b0z5f Net Yukuriddo Gojoho Kihon



3



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス




最重要 最大公約数 最少公倍数に関する難問 中学数学 理科 寺子屋塾の復習サイト




最大公約数と最小公倍数の積の性質の2通りの証明 高校数学の美しい物語




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学



覚えておきたい最小公倍数と最大公約数の求め方 盛り上がれ秋田



高校1年の数学について質問です42と63とnの最大公約数が21 最小 Yahoo 知恵袋




すごい最小 公倍数 問題




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質




最大公約数と最小公倍数のひみつ 苦手な数学を簡単に



最小公倍数と最大公約数から元の数を求めるには互いに素な数と共通因数が鍵 まぜこぜ情報局




大きな数の最大公約数の求め方 Youtube



48s96ub7b0z5f Net Saidaikouyakusuu Saisyoukoubaisuu




最大公約数が7 で 和が84 になる2 つの整数の組をすべて求めなさい Youtube




最大公約数と最小公倍数の求め方 2つの組 Youtube




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




2講 最大公約数 最小公倍数 1節 約数と倍数 問題集 3章 整数の性質




3講 最大公約数 最小公倍数の性質 1節 約数と倍数 問題集 3章 整数の性質




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




高校数a 整数 最大公約数 最小公倍数から数を求める オンライン無料塾 ターンナップ Youtube




倍数と約数 最小公倍数を求める 3つの数 Youtube



最高の公倍数 公約 数 子供のための最高のぬりえ




N 24 60の最大公約数が12 最小公倍数が1080のnをすべて求めよ という問 Clear




最重要 最大公約数 最少公倍数に関する難問 中学数学 理科 寺子屋塾の復習サイト
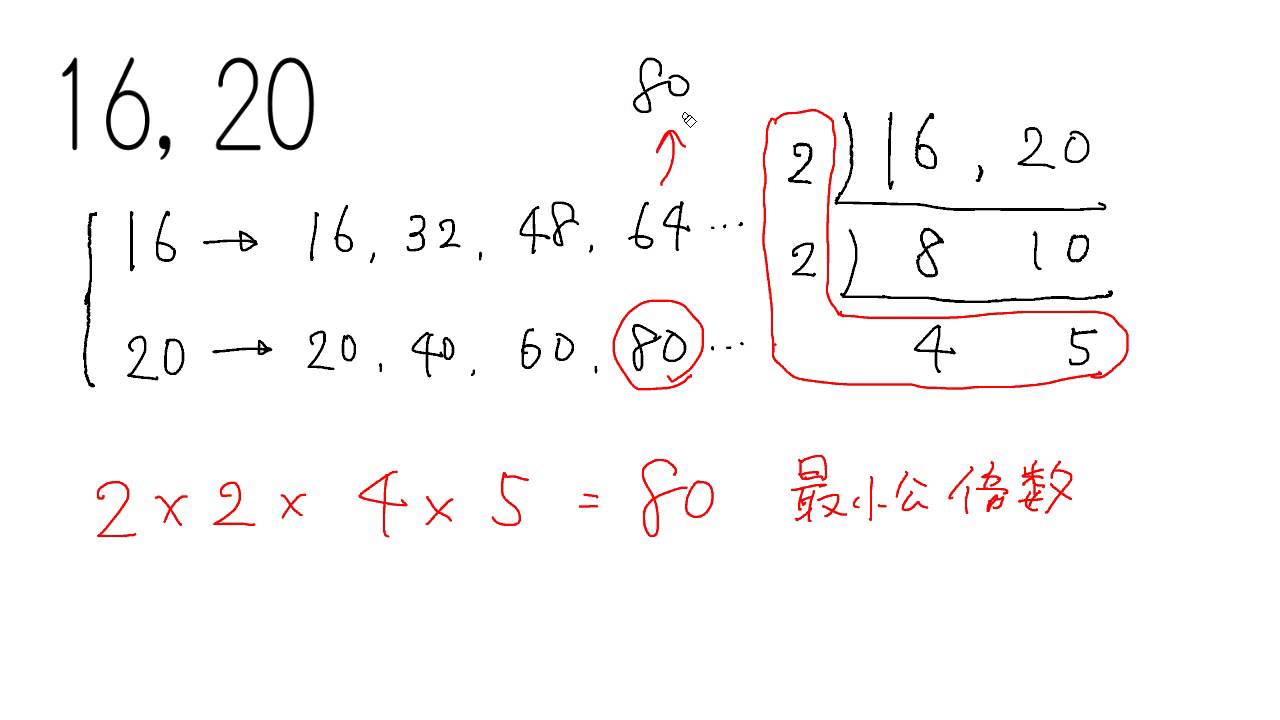



大きな数の最小公倍数の求め方 Youtube



最大公約数 最小公倍数




高校数学 最大公約数と最小公倍数 数学の問題が解けず困っています 数学 教えて Goo
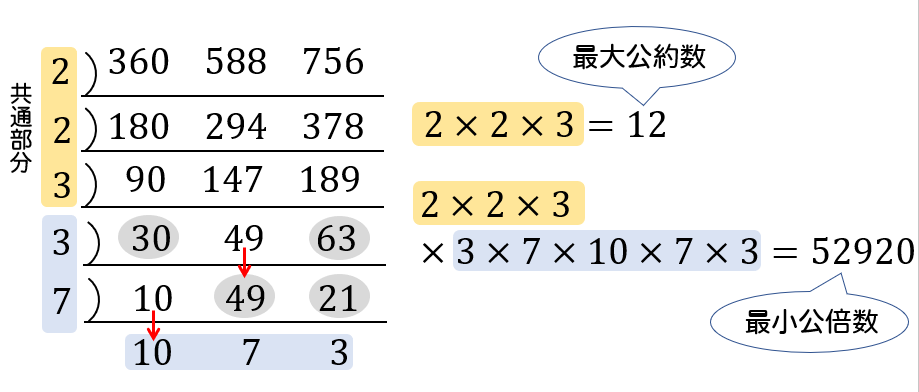



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
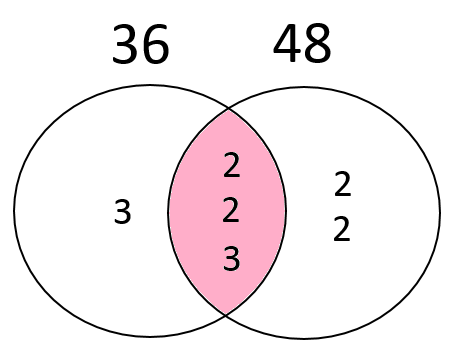



小学算数 最大公約数と最小公倍数を図を使って理解する 偏差値40プログラマー




整式とは 整式の最大公約数と最小公倍数の求め方




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座



最大公約数と最小公倍数




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




数学a 最大公約数と最小公倍数の求め方とコツ 教科書より詳しい高校数学




高校数学a 最小公倍数をヒントにnを求める問題 例題編 映像授業のtry It トライイット
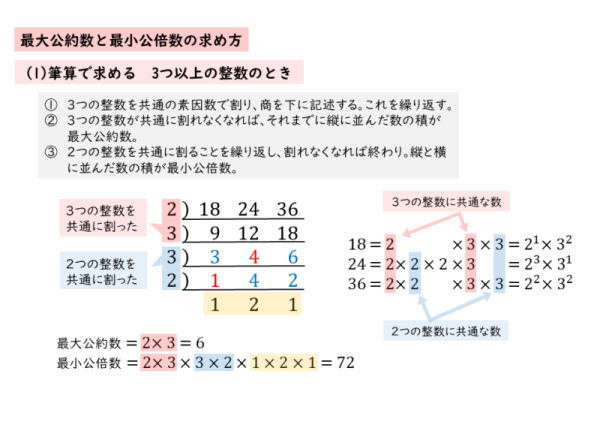



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん



最大公約数と最小公倍数の計算方法 高校数学マスター




249の問題が分かりません nをすべて求めよ という問題です Clear



整数の性質 最大公約数と最小公倍数について 日々是鍛錬 ひびこれたんれん




公約数 最大公約数 公倍数 最小公倍数 求め方 ぐらたん塾




小5 算数 小5 倍数 公倍数 最小公倍数 Youtube



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ



0 件のコメント:
コメントを投稿